mxnet二多类逻辑回归softmax

发表于 | 分类于 | 阅读次数:
字数统计: 1,216 | 阅读时长 ≈ 6

多类逻辑回归

1.其实就是一个多分类问题，用到softmax函数：将每一项变为非负，然后归一化每一项得到一个概率。(softmax虽然简单但是手写存在一点问题，当输入过大，出现NAN,除此之外易造成数值的不稳定)
2.另一种针对预测为概率值的损失函数—-交叉熵损失函数，关于交叉熵函数的详解.将两个概率的负交叉熵作为目标值，最小化这个值等于最大化这两个概率的相似度(预测概率和真实概率)。
3.数据集采用的FashionMnist，讲道理Mnist被用烂了吧。
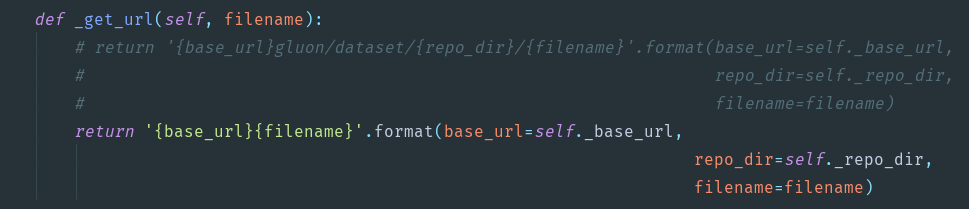
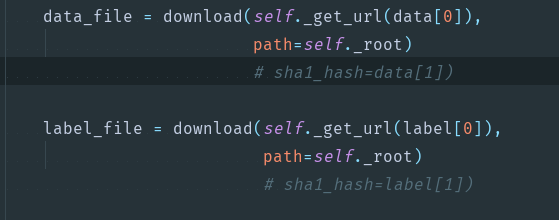
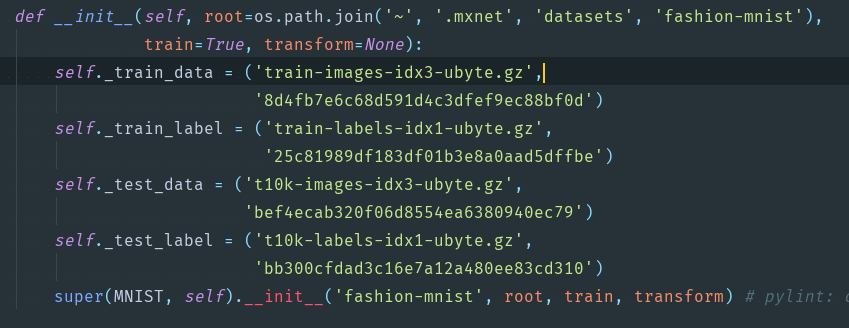
4.关于FashionMnist的下载问题。换下载地址。vision.py，需要改的部分上截图。下拉到文底

下载数据，制作数据迭代集

transform 对数据进行归一化，类型转换，用gluon制作数据迭代集

1
2
3
4
5
6
7
from mxnet import ndarray as nd
from mxnet import  autograd as ag
from mxnet import gluon
def transform(data,label):
    return data.astype('float32')/255,label.astype('float32')
mnist_train = gluon.data.vision.FashionMNIST(train=True,transform=transform)
mnist_test = gluon.data.vision.FashionMNIST(train=False,transform=transform)

设置输入维度和输出维度,为参数申请梯度空间

1
2
3
4
5
6
7
num_inputs = 784
num_output = 10
w = nd.random_normal(shape=(num_inputs,num_output))
b = nd.zeros(shape=num_output)
params = [w,b]
for param in params:
    param.attach_grad()

多分类函数

这是低级版的softmax，可以有一些优化
也可以理解为对计算结果的值域限制

1
2
3
4
def softmax(a):
    exp = nd.exp(a)
    partition = exp.sum(axis=1,keepdims=True)
    return exp/partition

网络计算

1
2
def net(x):
    return softmax(nd.dot(x.reshape((-1,num_inputs)),w)+b)

交叉熵损失函数(针对概率值的损失函数)

1
2
def cross_entropy(yhat,y):
    return -nd.pick(nd.log(yhat),y)

优化函数

1
2
3
def SGD(params,lr):
    for param in params:
        param[:] = param - lr*param.grad

计算准确率和evaluate_accuracy

这里的output是一个矩阵，第一维度是batch_size
这里的argmax返回output每行中最大值的索引
asscalar将nd.mean的结果转为标量

1
2
3
4
5
6
7
8
def accuracy(output,label):
    return nd.mean(output.argmax(axis=1)==label).asscalar()

def evaluate_accuracy(data_iterator,net):
    acc = 0
    for data,label in data_iterator:
        acc+=accuracy(net(data),label)
    return acc/len(data_iterator)

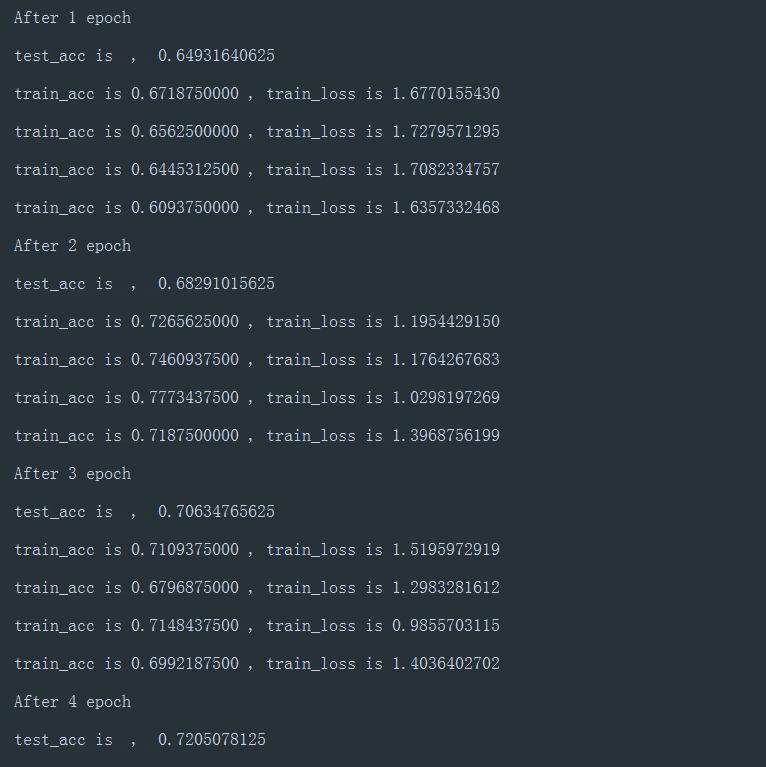
训练(打印没训练的模型准确率作为参考，一般接近10%)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
print('Not train ,the result',evaluate_accuracy(test_data,net))

epoch = 5
for e in range(epoch):
    i = 0
    for data,label in train_data:
        i+=1
        with ag.record():
            output = net(data)
            loss = cross_entropy(output,label)
        loss.backward()
        SGD(params,lr=0.0004)
        train_acc = accuracy(output,label)
        train_loss = nd.mean(loss).asscalar()
        if i%50==0:
            print('train_acc is %.10f , train_loss is %.10f'%(train_acc,train_loss))
    test_acc = evaluate_accuracy(test_data,net)
    print('After %d epoch'%(e))
    print('test_acc is  , ',test_acc)

截图

继续研究softmax问题

关于FashionMnist如何下载问题，下面提供自己的解决方案




不加解释上Gluon版本，识别率居然比自己写的高10个百分点，那是什么原因。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
from mxnet import ndarray as nd
from mxnet import autograd as ag
from mxnet import gluon
def transform(data,label):
    return data.astype('float32')/255,label.astype('float32')
mnist_train = gluon.data.vision.FashionMNIST(train=True,transform=transform)
mnist_test = gluon.data.vision.FashionMNIST(train=False,transform=transform)
batch_size = 256
train_data = gluon.data.DataLoader(mnist_train,batch_size,True)
test_data = gluon.data.DataLoader(mnist_test,batch_size,False)
# data,label = mnist_train[0]
# print(data.shape,label)
#定义网络
net = gluon.nn.Sequential()
with net.name_scope():
    #官网上的解释Flattens the input to two dimensional.
    net.add(gluon.nn.Flatten())
    net.add(gluon.nn.Dense(10))
net.initialize()
#定义损失函数分来定义softmax和交叉熵会有数值不稳定性，gluon提供了合起来的api
softmax_cross_entropy = gluon.loss.SoftmaxCrossEntropyLoss()
#优化器
trainer = gluon.Trainer(net.collect_params(),'sgd',{'learning_rate':0.1})

def accuracy(output,label):
    return nd.mean(output.argmax(axis=1)==label).asscalar()

def evaluate_accuracy(data_iterator,net):
    acc = 0
    for data,label in data_iterator:
        acc+=accuracy(net(data),label)
    return acc/len(data_iterator)

#开始训练
epoch = 5
for e in range(epoch):
    i = 0
    for data,label in train_data:
        with ag.record():
            yhat = net(data)
            loss = softmax_cross_entropy(yhat,label)
        loss.backward()
        trainer.step(batch_size)
        train_loss = nd.mean(loss).asscalar()
        i += 1
        if i%40==0:
            print('After %d epoch, train_loss is '%(e),train_loss/batch_size)
    acc = evaluate_accuracy(test_data,net)
    print('After %d epoch, test_acc is '%(e),acc)

补充

  1. 上面的softmax中会发生上溢出和下溢出，可以想象当x很大时，exp(x)会出现NAN情况，显然是不想看到的，可以用平移的思想。exp(x-max(X)),这样会用0取代先前的NAN。可是这还不是理想的状态…
  2. 机器学习中的训练其实是对损失函数(loss function)的优化。
  3. 分类问题中，一般使用最大似然估计来构造损失函数。最大化似然函数等同于最小化对数似然。
  4. 相对熵和交叉熵。交叉熵反映了p,q之间的相似程度。
  5. 对于分类问题，对数似然和交叉熵损失函数是等价的。