Purpose
这两周感觉效率偏低，GAN的论文看的迷迷糊糊还没有完全弄清楚，加上最近沉迷吃鸡，没有那个精力，心态（主要原因）去好好整一篇博客。所以…打算换个project来缓一缓断更的节奏。这个project是打算作为模式识别机器学习课程的一篇报告。说起这个课脑袋就很疼，一只脚踏入了挂科的深渊，希望自己能够吸取教训。这个project是kaggle上的一个竞赛，有7万刀。虽然已经结束了内容也比较简单，但应该是一个不错的入门案例。
Model
Bagging and RandomForest
在机器学习中为了得到强泛化性能的集成，个体学习器应尽可能的相互独立，即基学习器尽可能具有较大的差异。主要的做法是：给定一个训练数据集采样出若干个不同的子集，在子集的基础上训练分类器。需要的注意的是子集的数量不能太小否则无法进行有效的学习，又要满足独立的原则，所以一般使用相互有交叠的采样子集。
Bagging
- 并行式集成学习方法的一种，假如采样出$T$个含$m$个训练样本的采样集，然后基于每个采样集训练出基学习器，再将基学习器结合。
- Bagging是对分类任务使用简单投票法，对回归使用简单平均法，票数 相同随机选择一个。
- Bagging和Adaboost有一个不同的地方，标准Adaboost只适用于二分类任务，Bagging能够不改地用于多分类和回归任务。
看下训练算法：
Decision Tree
关于决策树算法这块，这边不打算展开叙述（直观理解还是需要例子加以辅助，推荐周志华的西瓜书，浅显易懂）。只说明大体上决策树的组成和重要的知识点。
做决策的树形模型，一般的，一棵决策树包含一个根节点，若干个内部节点和若干个叶节点。叶节点对应于决策结果，其他结点对应熟悉你个测试，每个结点包含的样本集合根据属性测试的结果被划分到子节点中，根节点包含样本全集。基本思想‘分而治之’，基本思想如下：
purity
根据算法可知，构建决策树的重点在于属性的划分。属性的划分依据是结点的纯度，希望决策树的分支结点包含的样本尽可能属于同一类别，即纯度越高越好。纯度有不同的衡量标准：
information gain
information entropy信息熵，信息量的期望，度量样本集合纯度最常用的指标。信息量：事件发生带来的信息大小（一个事件发生的概率越大包含的信息量越少）。对于集合$D$,信息熵的定义为：
$Ent(D)$的值越小，则D的纯度越高。
假定离散属性$\alpha$有$V$个可能的取值${\alpha^1,\alpha^2,…,\alpha^V}$,若使用$\alpha$对样本集划分，则会产生$V$个分支结点，其中第$v$个分支结点包含了$D$中所有在属性$\alpha$上取值为$\alpha^v$的样本，记为$D_v$。考虑到不同的分支节点包含的样本数不同，给分支节点赋予权重$\partial{|D^v|}{|D|}$,样本数越多的分支结点的影响越大，则属性$\alpha$对样本集$D$进行划分所获得的信息增益为：
这里信息增益越大，一直意味着按照属性$\alpha$来进行划分所获得的‘纯度提升’越大。那么选择属性的原则按照$\alpha^*=argmax Gain(D,\alpha)$ID3决策树就是按照信息增益为准则来选择划分属性。
gain ratio
刚才说到的信息增益有一个问题，信息增益准则对可取值数目较多的属性有所偏好。大概的理解是 ：每个属性分支结点包含的样本少，则说明纯度大。例如将数据的编号作为划分属性，每个属性分支节点只有一个样本，纯度达到最大，然而这样的决策树泛化能力为0。因此有些决策树使用增益率来选择最有划分属性。如：C4.5。增益率定义为：
其中
称为属性$\alpha$的固有值，属性$\alpha$可能取值数目越多（$V$越大），则$IV(\alpha)$的值越大。
gini index
基尼指数是CART决策树。
直观上$Gini(D)$表示的意义是：从数据集$D$中随机抽取两个样本，其类别标记不一致的概率，$Gini(D)$越小，则数据集$D$的纯度越高。属性$\alpha$的基尼指数定义为
pruning
减枝是决策树学习为了防止过拟合的手段，主要原因是，为了正确分类样本，划分过程不断重复，造成决策分支过多样本学得太好而导致。决策树的减枝基本策略“预减枝”，“后剪枝”。
- 预减枝：在决策树生成过程中，对每个结点在划分前先进行估计，若当前结点的划分布恩那个带来决策树泛化性能提升，则停止划分将该节点标记为叶节点
- 后剪枝则是先从训练集生成一棵完整的决策树，然后自底而上地对非叶子结点进行考察，若将该结点对一个的子树替换成叶结点能带来决策树泛化性能提升，则将该子树替换成叶节点。
上面说的两种减枝方法比较抽象，可以参考周志华的西瓜书，有例子能够更加直观。
continuous values
遇到连续属性，应该如何划分属性呢？C4.5采用的是二分法对连续值进行处理。给定样本集$D$,假定$\alpha$在$D$上出现了$n$个不同的取值，将这些值从小到大进行排序，记为${\alpha^1,\alpha^2,…,\alpha^n}$,基于划分点$t$可将$D$分为子集$D_t^-$和$D_t^+$，前者包含属性$\alpha$上取值不大于$t$的样本，后者表示大于$t$的样本。在连续属性$\alpha$上可考察包含$n-1$个元素划分集合：
划分后计算划分依据标标准，与其他属性一起比较。需注意的是，于离散属性不同，若当前结点划分属性为连续属性，该属性还可作为其后代结点的划分属性。
Random Forest
- RF是Bagging的一个扩展变体，RF的基学习器是一个决策树。但是RF在Bagginig的基础上，在决策树的训练过程中引入了随机属性选择。
- 传统decision tree在选择划分属性的原则是当前属性结点的属性集合中选择一个最优属性，在RF中，对每个基决策树的每个结点，从该结点的属性集合中随机选择包含$k$个属性的子集，再从子集中选择一个最优属性用于划分，参$k$控制了随机性的引入程度，推荐是$k=log_2d$。
- RF思想简单，容易实现，计算开销小，却有展现除强大的性能。RF对Bagging做了小改动，不仅有来自样本的扰动（Bagging），还有属性的扰动（Decision Tree)这样使得集成的泛化性能可通过个体学习器之间差异度进一步提升。
- RF和Bagging的收敛性相似，但是RF的起始性能往往较差，但是随着学习器的数目增多RF能够收敛到更低的泛化误差。
combined strategy
学习器的结合策略的好处：
- 统计来说：学习任务的假设空间很大，多个假设在训练数据集上达到同等性能，此时单学习器就会出现弊端，导致泛化性能不佳。
- 计算来说：学习算法往往会陷入局部极小，局部极小对应的泛化性能差。
- 表示来说：学习任务假设可能不在当前学习算法假设空间，此时的单学习器无效。
常见结合策咯： - 平均值：简单平均值，加权平均值
- 投票法：绝大多数投票法，相对多数投票法，加权投票法
- 学习法：是通过另一个学习器来进行结合。Stacking是学习法的典型代表。个体学习器称为初级学习器，用于结合的学习器成为次级学习器或元学习器。次级训练数据集不采用初级训练集所用的样本，一般使用交叉验证这样的方式。
Liner model
所谓线性模型在给定d个属性描述的示例$x=(x_1;x_2;…x_d)$,通过属性的线性组合来进行预测。
线性模型虽然简单，但是很多强大的非线性模型是在线性模型的基础上引入层级结构（深度神经网络）和高维映射（SVM等）得到。
Linear Regression
线性回归是线性模型在回归任务下的一种应用，输出值是一个连续值。线性回归的模型参数就是线性模型的$W,b$,那么如何学习$W,b$呢？需要一个目标函数，使得在$W,b$的作用下，预测值$f(x)$接近真实值$y$，目标函数有很多，在线性回归任务中常用的是均方误差
均方误差对应了欧几里得距离，基于均方误差最小化进行模型求解的方法称为‘最小二乘法’。几何意义：试图找到一条直线，使所有样本到直线上的欧氏距离之和最小。给出目标函数$E_{(w,b)}=\sum_{i=1}^m(y_i-wx_i-b)^2$,该误差函数是关于$w,b$的凸函数，当$w,b$的导数为零时，得到最优解。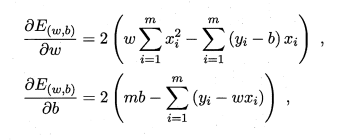
更为一般的转为矩阵形式：试图学习
继续利用最小二乘法对$w,b$进行估计，为了方便矩阵的直接相乘把$w,b$和在一起$w^T=(w;b)$,相应地把数据集D表示d(属性)+1维的矩阵。
新的目标函数为：
对$w$求导得到
当$X^TX$为满秩矩阵或正定矩阵时有
但$X^TX$并非时时都是满秩的，这会导致求出多个$w_*$,都能使得均方误差最小化，通常选择哪一个解是由算法的归纳偏好决定的，常见方法引入正则化。
除此之外，让线性模型逼近于y的衍生物，实质上时求取输入空间到输出空间的非线性函数映射。如对数线性回归：
是让$e^{w^Tx+b}$，更为一般地，考虑单调可微函数$g()$
广义线性模型。
Logistic Regression
上面说的是线性模型做回归任务，如果是分类任务呢？基于刚才的广义线性模型，只需要找到一个单调可微函数将真实标记$y$和模型预测值$f(x)$联系起来即可。对于二分类输出空间0或1，将上述的线性回归模型$z=w^Tx+b$得到的实值转换到0/1的值，理想的函数是‘单位阶跃函数’。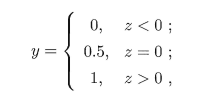
，但是该函数不连续啊！前人就找到了logistic function。
sigmoid函数
将该形式转化一下：
其中$y$可视为样本x作为正例的可能性，$1-y$则视为其反例的可能性，$\frac{y}{1-y}$称为几率，表示$x$作为正例的相对可能性。
Logistic Regression Advantage
- 虽然是英文叫Logistic Regression,但是一个分类任务。
- 该学习器是直接对分类可能性建模，不需要假设数据分布，避免了假设分布不准确的问题。
- 它不仅预测出类别，而且得到的近似概率预测，这样有助于利用概率辅助决策的任务。
- 对率函数是任意阶可导的函数，有许多数值优化算法可直接用于求取最优解。
Logistic Regression and loglikehood
将$y$视为后验概率，前式子
可转换为
且有
通过‘极大似然法’来估计$w,b$
令每个样本属于器真实标记的概率越大越好，进一步将上式中的似然项改写（为了方便$\beta=(w,b),x=(x,1)$）$,则$w^Tx+b$简写为$\beta{^T}x$
是不是有点交叉熵的感觉，留下一个伏笔。
Linear Discriminant Analysis
本来不打算写这个方法的，但是比较简单，那就一笔带过吧。
LDA不严格的来说就是‘Fisher判别分析’，思想比较简单：给定训练集，设法将样例投影到一条直线（对应二维来说），目标是：同类的投影点尽可能靠近，异类的点尽可能远离。对于测试样本，先投影再根据投影点的位置来确定新样本的类别。如图：
Math representation
对于数据集$D$，二分类任务为例：有$X_i,\mu_i,\sum_i$分别表示第i类示例的集合，均值向量，协方差矩阵。若将数据投影到直线$w$上，则两类样本的中心在直线上的投影分别为$w_T\mu_0$和$w_T\mu_1$,对于所有样本点投影，样本的协方差分别为$w^T\sum_0w$和$w^T\sum_1w$。上述同类样本点的投影点应该尽可能接近，意味着投影点的协方差尽可能小，即：$w^T\sum_0w+w^T\sum_1w$尽可能小。异类样本投影点尽可能远离，意味着异类中心点之间的距离尽可能大，即$||w_T\mu_0-w_T\mu_1||_2^2$。有了这样的分析，可能到目标函数：
最大化J即为所求。
剩下的一些就是在编程序时减少计算的量的求解，用到的知识：矩阵性质，拉格朗日乘子法，奇异值分解。参考周志华的西瓜书。
SVM
占坑
Dimension reduction
- 提供点的坐标进行降维 PCA
- 点之间的距离矩阵 MDS
MDS
由原始样本的距离矩阵 D 到样本的内积矩阵 B ，然后对 B 进行特征值分解，得到小于等于N个特征值和特征矩阵，构造降维后的样本矩阵 Z。
Linear Dimension reduction
$z_i$是原属性向量$x_i$在新坐标系${w_1,w_2,\cdots,w_d}$中的向量坐标。新空间中的属性是原空间属性的线性组合。这是线性降维的基本形式，不同线性降维对低维子空间的性质有不同的要求，相当于对$W$有不同的约束。
PCA
Principal Component Analysis 从最近重构性或者最大可分性都能得到主成成分分析的推导。最大可分性：样本点$x_i$在新空间中超平面上的投影是$W_TX_i$,若所有样本点的投影尽可能分来，应使得投影后样本点的方差最大化。投影后的样本方差
优化函数变为：
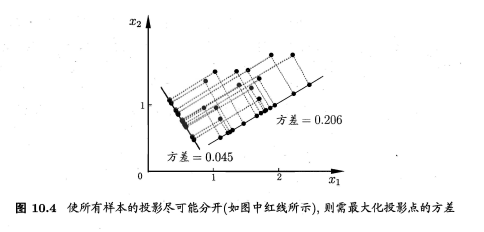
只需对协方差矩阵$XX^T$进行特征值分解，将求得的特征值排序,再取$d$个特征值对应的特征向量构成$W$,即为主成成分的解。降维后的维度$d$,或者用开销较小的分类器子在交叉验证中选取。